포물선

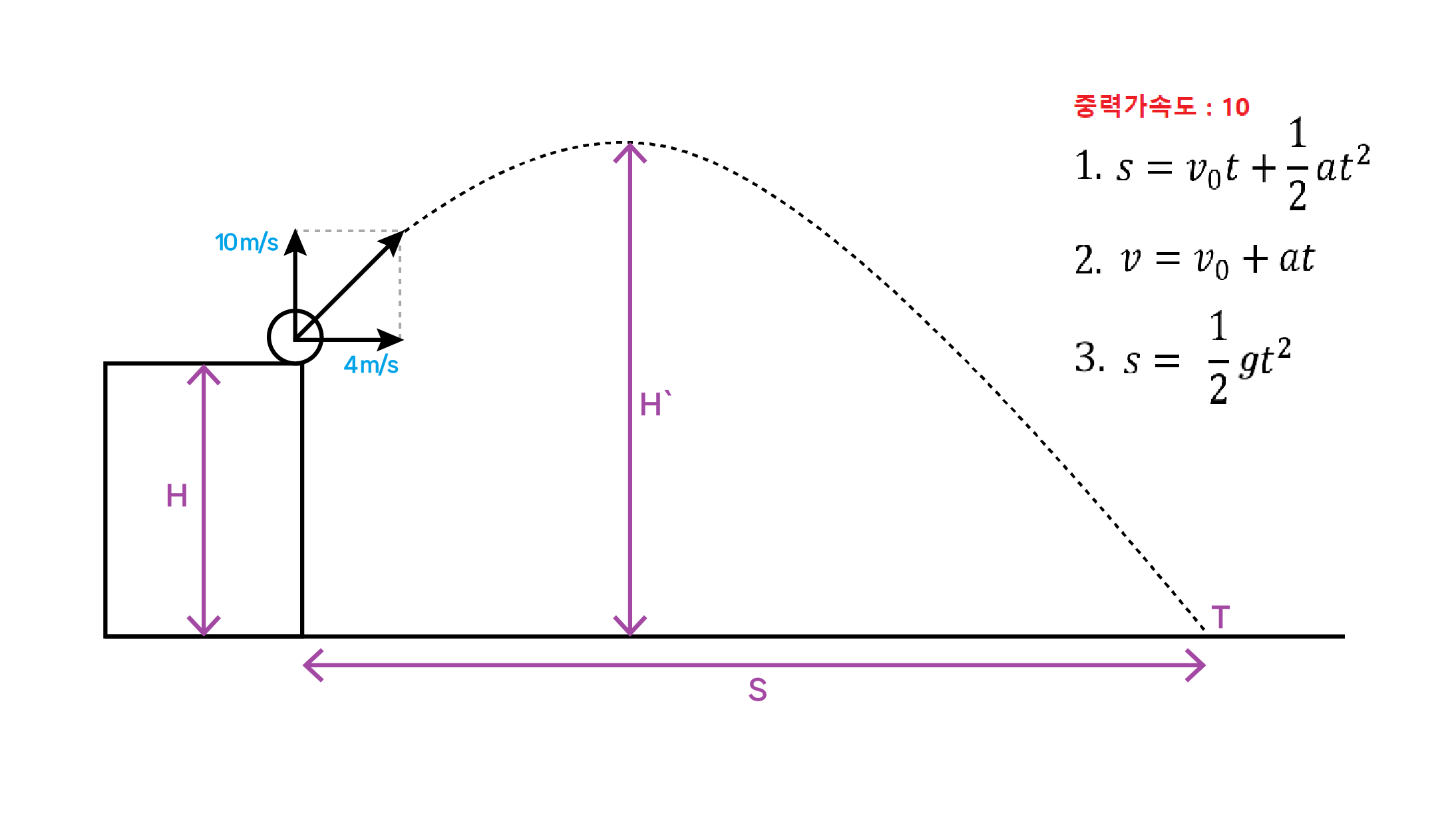
그림 상황에서 공이 지면에 닿을 때 까지 걸린 시간(T)을 구하려고 한다.

---

공식

두 가지 방법이 있다.

1. 등가속도 운동공식 이용.
2. 올라가는 시간(등속도 운동공식)과 떨어지는 시간(자유낙하 공식) 두 가지로 나눠서 구하기.

등가속도 운동공식	\(s = v_0 t + \frac{1}{2} a t^2\)
등속도 운동공식	\(v = v_0 + at\)
자유낙하 공식	\(s = \frac{1}{2}gt^2\)

---

수학 공부에 소홀히했던 지난 날을 후회한들 뭐하리, 일단 내가 막히는 부분부터 알아보겠다.
공식은 검색만 해도 금방 찾을 수 있지만 의미를 모르겠는 기호의 압박이 심하다.

S	공이 이동한 거리
V0	공의 처음 속도 (수직 방향 속도. 예시 상황에선 10m/s)
a	가속도(acceleration) (여기선 중력가속도를 의미)
t	시간

공식을 풀어서 읽어보면 아래와 같다.

공이 이동한 거리 = (공의 처음 속도 * 시간) + (1/2 * 중력가속도 * (시간 * 시간))

---

이차방정식의 해는 근의 공식을 이용해 구할 수 있다.

\[x = {-b \pm \sqrt{b^2-4ac} \over 2a}\]

---

풀이 과정

1. 등가속도 운동공식에 대입

• 높이 H는 더한다.

\[\begin{aligned} S &= H + v_0 t + \frac{1}{2} a t^2 \\ S &= H + 10t + \frac{1}{2} \cdot (-10) \cdot t^2 \\ S &= H + 10t - 5t^2 \end{aligned}\]

2. 위치가 0일 때 (지면 도달)

\[\begin{aligned} 0 = H + 10t - 5t^2 \\ 5t^2 - 10t - H = 0 \end{aligned}\]

3. 근의 공식 사용

\[\begin{aligned} t &= \frac{-(-10) \pm \sqrt{(-10)^2 - 4 \cdot 5 \cdot (-H)}}{2 \cdot 5} \\ &= \frac{10 \pm \sqrt{100 + 20H}}{10} \\ &= 1 \pm \frac{\sqrt{100 + 20H}}{10} \end{aligned}\]

---

만약 H = 10 이라면?

1. H = 10 대입

\[\begin{aligned} t &= 1 \pm \frac{\sqrt{100 + 20H}}{10} \\ &= 1 \pm \frac{\sqrt{100 + 20 \cdot 10}}{10} \\ &= 1 \pm \frac{\sqrt{100 + 200}}{10} \\ &= 1 \pm \frac{\sqrt{300}}{10} \\ \end{aligned}\]

2. √300 간단히 하기

\[\begin{aligned} \sqrt{300} &= \sqrt{100 \cdot 3} \\ &= \sqrt{100} \cdot \sqrt{3} \\ &= 10\sqrt{3} \end{aligned}\]

3. 정리

\[\begin{aligned} &= 1 \pm \frac{10\sqrt{3}}{10} &= 1 \pm \sqrt{3} \end{aligned}\]

4. 최종 해

\[\begin{aligned} t &= 1 \pm \sqrt{3} \\ &\approx 1 \pm 1.732 \\ &\Rightarrow t_1 \approx 2.732,\quad t_2 \approx -0.732 \end{aligned}\]

즉, H = 10이면 공이 지면에 닿을 때 까지 걸린 시간은 약 2.732초다.